Iloa ja ymmärrystä matematiikkaan!

Iloa ja ymmärrystä matematiikkaan!
Päivitetty 25.2.2007
© 2022 Hannele Ikäheimo
Kysyjän ensimmäinen kirje Hannelen ensimmäinen vastaus Hannelen täydennys edelliseen Kysyjän lisäkysymys Hannelen vastaus Kysyjän kommentit Hannelen loppukommentit
Laskutaito-kirjasarjan 4. luokan kevätosa tarjosi heti lukukauden alkajaisiksi upean yllätyksen: jakolaskua allekkain, hyvä! Jo joutaa romukoppaan kaiken maailman jakokulmakyhäelmät; nyt jakolaskukin on alusta loppuun lauseke, kauniilla matematiikan kielellä ilmaistu. Itse opetan 5.–6. -luokan matematiikkaa ja otan tällä päivämäärällä käyttööni kyseisen jakolaskutavan.
Minua askarruttaa kuitenkin seuraava didaktinen kysymys: esim.
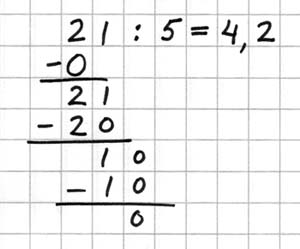
Miten selitän lapsille mistä 0 tipautetaan ykkösen viereen? Tietysti sen voisi jo alussa merkitä muotoon 21,0 : 5, mutta sehän jo edellyttää tietoa, ettei jakolasku mene tasan, mitä lapsilla ei välttämättä vihkoon laskua merkitessään ei ole. Em. oppikirjassa jakolaskuja ei laskettu loppuun saakka, vaan jätettiin jakojäännös, aivan kuin 4.-luokan OPS:n mukaan kuuluukin tehdä. Miten toimin?
Jo etukäteen vastauksesta nöyrimmät kiitokseni.
t. "Kysyvä ei jakokulmaa käytä".
∼ ∼ ∼ ∼ ∼ ∼
Kiitos mielenkiintoisesta kysymyksestäsi!
Ihan aluksi: Oletko lukenut artikkelini Jakolaskuun ymmärrystä, joka löytyy www.opperi.fi-sivuilta Opetusvinkkien kohdasta Luvut ja laskut?
1. vastaus:
Ongelmasi paljastaa puutteen uudessa tavassa jakaa allekkain: kokonaisluku-jaettavan perään ei
mahdu kirjoittamaan tarvittavaa desimaalipilkkua eikä nollia. Tätä puutetta ei ole ruotsalaisessa
jakokulmassa, joka on artikkelini 3. kuvassa (alusta lukien). Siis edelleenkin on ymmärtäminen
tärkeintä – siitä alla olevissa vastauksissa lisää.
2. vastaus:
Ongelmasi johtuu myös siitä, että jaettava 21 on liian pieni, kun tavoitteena on opetella uusi tapa
suorittaa jakolaskua allekkain. Oppikirjoissa valitettavasti aloitetaan liian pienillä luvuilla,
mutta sehän ei estä ottamasta yhteiseen käsittelyyn muuta aloitustapaa. Tärkeintä tässäkin on
YMMÄRTÄMINEN!!!
Jakolaskun 408 : 2 voi ensin havainnollistaa joko 10-järjestelmävälineillä tai ainakin rahoilla (408 euroa jaetaan tasan kahdelle). Sen jälkeen jakolasku suoritetaan lyhyellä tavalla (ks. artikkelini) ja sitten uudella tavalla allekkain. Suosittelen lukuyksikköjä vastaavien KIRJAINTEN merkitsemistä sekä JAETTAVAN että OSAMÄÄRÄN yläpuolelle (eli tässä tapauksessa SKY) (ks. artikkelini 5. kuva).
3. vastaus:
Eihän jakolaskua 21 : 5 tarvitse missään allekkainlaskumuodossa tai jakokulmassa jakaa!
YMMÄRTÄMINEN on taas tärkeää: konkreettiset palikat ja tarinat avuksi, kun opsissakin mainitutuja
ositus- ja sisältöjakoja selvennetään (sekä oppilaille että opettajille):
- OSITUSJAKO: "21 karkkia jaetaan 5 lapselle tasan. Kuinka monta karkkia kukin saa? Jääkö yhtään
karkkia jakamatta?"
- SISÄLTÖJAKO: "21 karkkia jaetaan tasan niin, että kukin lapsi saa 5 karkkia. Kuinka monelle
lapselle karkit riittävät? Jääkö yhtään karkkia yli?"
Iloisin terveisin
:-) Hannele
∼ ∼ ∼ ∼ ∼ ∼
Enpähän saanut äsken vastausta kokonaan valmiiksi, huomasin sen sauvakävelyllä. Tässä lisää...
4. vastaus:
Kun kokonaisluku on jaettavana ja jako ei mene tasan, eikä jakojäännös riitä vastaukseksi,
osamäärään tulee desimaalilukuja. Miten tähän saadaan ymmärrystä? Tarinoiden ja rahojen avulla,
esimerkiksi. Ositusjakotarina: "21 euroa jaetaan 5 oppilaalle tasan. Jakamatta jää 1 euro. Entä jos
se euro muunnetaan senteiksi, voidaanko jakoa jatkaa? Kyllä. Jne."
Alkuperäinen rahamäärä merkitään eri kohtaan valmiiksi muotoon 21,00 ja yläpuolelle kirjoitetaan lukuyksikkö-kirjaimet: K Y , ko so. Samoin osamäärän paikalle ruutujen yläpuolelle, jolloin samalla puhutaan: "Tähän tulevat kympit, tähän ykköset, tähän euron kymmenesosat eli 10 senttisten lukumäärä ja lopuksi euron sadasosat eli senttien lukumäärä."
Huom. sisältöjakotarinasta ei saada luontevaa ratkaisua, jossa on desimaaliluku; siihen tarinaan riittää hyvin jakojäännös: "21 euroa jaetaan oppilaille niin, että kukin saa 5 euroa. Kuinka monelle rahat riittävät?" "4 oppilaalle ja jakamatta jää 1 euro."
Odotan mielenkiinnolla kommenttiasi!
:-) Hannele
∼ ∼ ∼ ∼ ∼ ∼
Olen tutustunut mainitsemaanne aineistoonne netissä. Siellähän tuo oli koko jakolaskun historia vähän laajemminkin esitelty. Tämä historia on mielestäni ihan hyvä esitellä yksinkertaisten esimerkkien valossa oppilaille, vanhemmille ja opettajakolleegoille, silloin ennakkoluulot häviävät ja asia menee eteenpäin. Mitä tulee tuohon esittämääni didaktiseen ongelmaani, niin esimerkkini oli huono, mutta onneksi asia tuli selväksi. Noin sen minäkin olisin ratkaissut.
Peräsin vain tietoa siitä, että onko esim. unkarilaisessa matematiikassa jokin merkintätekninen tms. seikka, jossa niille kymmenys- ja sadasosille todellakin jäisi tilaa jaettavan kokonaisien perään? Näin koko lasku olisi kerralla nätisti paketissa, kauniilla matematiikan kielellä.
t. "Kysyvä ei jakokulmaa käytä"
∼ ∼ ∼ ∼ ∼ ∼
Kiitos vastauksestasi.
Lisäkysymyksesi oli hyvä. Unkarissa ei jätetä ennakoivasti tilaa jaettavan ja jakomerkin (:) ja jakajan väliin – eikä tietääkseni muuallakaan. Kun kokonaiset loppuvat, merkitään desimaalipilkku osamäärään ja lisätään nollia alas ihan niinkuin sinun esimerkissäsi.
Lukuyksikköjä vastaavia kirjainmerkintöjä ei tietääkseni käytetä muualla. Minä olen niitä kaikkien oppilaiden kanssa käyttänyt, ovat luopuneet niistä sitten kun ymmärtävät mistä on kyse. Kirjassani "Iloa ja ymmärrystä matematiikkaan" olen myös käyttänyt noita kirjaimia sekä konkreettisten välineiden alustoissa että vastaavissa lukumerkinnöissä ja laskuissa.
Mukavaa lumista ja kohta vaalenevaa talvea!
:-) Hannele
∼ ∼ ∼ ∼ ∼ ∼
Suuri kiitos vastauksestasi. Tällä tietämyksellä jaamme nyt ja tulevaisuudessa.
Loppukevennys:
Näin entistä työkaveriani, joka on iät ajat ollut sivutoimisena ravintolamuusikkona. Nyt hän soitti
koskettimia rytmikoneen onton äänen säestyksellä.. Hämmästellen kysyin häneltä:
-Eikö sinun bändissäsi ollut ennen myös haitaristi?
-Kuule, muistathan jakolaskun vanhan säännön; kun jakaja pienenee niin osamäärä suurenee,
jaettavahan pysyy näissä hommissa samana, sanoi kaverini ja antoi rumpukoneesta alkutahdit
tanssiyleisölle.
Hyvää jatkoa!
t. "Kysyvä ei jakokulmaa käytä"
∼ ∼ ∼ ∼ ∼ ∼
Heh, heh, kiitos hauskasta tarinasta, jonka voi kertoa koulutuksissa. Lähden taas kiertämään Suomea, ensin Rovaniemelle ja sitten Joensuuhun. Matikan oppimisvaikeudet ovat ilmeisesti räjähtämässä käsiin, koska tarvetta juuri noihin koulutuksiin on niin paljon. Itse pidän paljon koulutustilaisuuksista, jonne opet eivät tule pakolla (lue Veso-päivä). Niistä päivistä opin aina paljon itsekin...
... niinkuin tästä kysymyksestäsikin: vastaa lyhyesti ja itse ydinasiaan. Kiitos!
:-) Hannele